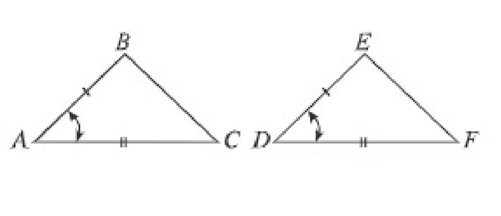
একটি ত্রিভুজকে অপর একটি ত্রিভুজের উপর স্থাপন করলে যদি ত্রিভুজ দুটি সর্বতোভাবে মিলে যায়, তবে ত্রিভুজ দুটি সর্বসম হয়। সর্বসম ত্রিভুজের অনুরূপ বাহু ও অনুরূপ কোণগুলো সমান। নিচের ABC ও DEF সর্বসম।
ABC ও DEF সর্বসম হলে এবং A, B, C শীর্ষ যথাক্রমে D, E, F শীর্ষের উপর পতিত হলে AB = DE , AC = DF BC = EF
∠ A = ∠ D ∠ B = ∠ E ∠ C = ∠ F হবে।
ABC ও DEF সর্বসম বোঝাতে ABC ≅ DEF লেখা হয়।
ত্রিভুজের সর্বসমতা প্রমাণের জন্য কী তথ্য প্রয়োজন? এ জন্য দলগতভাবে পরের পৃষ্ঠার কাজটি কর:
| কাজ ১। ∆ABC একটি ত্রিভুজ আঁক যেন AB =5 সে.মি., BC=6 সে.মি.এবং ∠B=60° হয়। (ক) ত্রিভুজের তৃতীয় বাহুর দৈর্ঘ্য এবং অন্য কোণ দুটি পরিমাপ কর। (খ) তোমাদের পরিমাপগুলো তুলনা কর। কী দেখতে পাচ্ছ? |
উপপাদ্য ১ (বাহু-কোণ-বাহু উপপাদ্য)
যদি দুটি ত্রিভুজের একটির দুই বাহু যথাক্রমে অপরটির দুই বাহুর সমান হয় এবং বাহু দুটির অন্তর্ভুক্ত কোণ দুটি পরস্পর সমান হয়, তবে ত্রিভুজ দুটি সর্বসম হয়।
বিশেষ নির্বচন: মনে করি,
বিশেষ নির্বচন: মনে করি,
ABC ও DEF এ AB = DE AC = DF এবং অন্তর্ভুক্ত ∠ BAC = অন্তর্ভুক্ত ∠ EDF প্রমাণ করতে হবে যে, ABC ≅ DEF
প্রমাণ
ধাপ | যথার্থতা |
| (১) ∆ABC কে Delta*DEF এর উপর এমনভাবে স্থাপন করি যেন A বিন্দু D বিন্দুর উপর ও AB বাহু DE বাহু বরাবর এবং DE বাহুর যে পাশে F আছে C বিন্দু ঐপাশে পড়ে। এখন AB = DE বলে B বিন্দু অবশ্যই E বিন্দুর উপর পড়বে। | [ বাহুর সর্বসমতা] |
| (২) যেহেতু angle BAC = angle EDF এবং AB বাহু DE বাহুর উপর পড়ে, সুতরাং AC বাহু DF বাহু বরাবর পড়বে। | [কোণের সর্বসমতা] |
| (৩) AC = DF বলে C বিন্দু অবশ্যই F বিন্দুর উপর পড়বে। | [ বাহুর সর্বসমতা] |
(৪) এখন B বিন্দু E বিন্দুর উপর এবং C বিন্দু F বিন্দুর উপর পড়ে বলে BC বাহু অবশ্যই EF বাহুর সাথে পুরোপুরি মিলে যাবে। অতএব, ABC, DEF এর উপর সমাপতিত হবে। ABC ≅ DEF (প্রমাণিত) | [দুটি বিন্দুর মধ্য দিয়ে একটি মাত্র সরলরেখা অঙ্কন করা যায়।] |
উদাহরণ ১। চিত্রে, AO = OB, CO = OD
প্রমাণ কর যে, ∆AOD ≅ ∆BOC
প্রমাণ: ∆AOD এবং ∆BOC এ
AO = OB, CO = OD দেওয়া আছে
এবং তাদের অন্তর্ভুক্ত ∠AOD = অন্তর্ভুক্ত ∠BOC
[বিপ্রতীপ কোণ পরস্পর সমান]।
∴ ∆AOD = ∆BOC [বাহু-কোণ-বাহু উপপাদ্য) (প্রমাণিত)
যদি কোনো ত্রিভুজের দুটি বাহু পরস্পর সমান হয়, তবে এদের বিপরীত কোণ দুটিও পরস্পর সমান হবে।
বিশেষ নির্বচন: মনে করি, ABC ত্রিভুজে AB = AC।
প্রমাণ করতে হবে যে, ∠ABC = ∠ACB
অঙ্কন: BAC এর সমদ্বিখণ্ডক AD আঁকি যেন তা BC কে D বিন্দুতে ছেদ করে।
প্রমাণ: ∆ABD এবং ∆ACD এ
(১) AB = AC (প্রদত্ত)
(২) AD সাধারণ বাহু এবং
(৩) অন্তর্ভুক্ত ∠BAD = অন্তর্ভুক্ত ∠CAD (অঙ্কনানুসারে)
সুতরাং ∆ABD ≅ ∠ACD (বাহু-কোণ-বাহু উপপাদ্য
∴ . ∠ABD = ∠ACD অর্থাৎ, ∠ABC = ∠ACB (প্রমাণিত)
common.read_more
common.or
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
